Innocent Until Proven Guilty: Hypothesis Test

Innocent Until Proven Guilty: Hypothesis Test: Each of us makes important decisions that shape our lives, every day.  We try to make the best decisions possible and yet, as the adage goes “all predictions of the future are wrong, some are just less wrong than others.”  Sometimes decisions are made in split seconds, while other times many long hours are spent pondering options and weighing pros and cons.  One of the most “enjoyable” parts of decision-making comes afterward…when everyone (it seems) judges whether we were right or wrong.  When I’m “right,” it’s because I’m a genius and when I’m wrong…I would have been right if I’d had all the information.

Leaders must arrive at decisions using scientifically sound reasoning, such as that found within Six Sigma improvement methodology.  While their command of data type, sample plan and measurement system principles are also necessary, effective decision-making most fundamentally depends on a deep understanding of the “Hypothesis Test.”

In general, a Hypothesis Test is a process that uses sample data to evaluate two mutually exclusive statements about a population.  Those statements are themselves hypotheses, i.e., “null hypothesis” and “alternative hypothesis.”  The outcome of the Hypothesis Test is an evidence-based decision to either accept the null hypothesis or reject it in favor of the alternative hypothesis.

Consider a criminal case within the United States’ legal system.  Working together, the prosecutor, defense attorney, judge, and jury are responsible for assuring a “fair trial”; i.e., that a valid hypothesis test is performed.  The null and alternative hypotheses are designated as, “Not Guilty” and “Guilty,” respectively, to reflect the fundamental presumption of innocence enjoyed by every defendant; Rules of Evidence, honed over many years and enforced by the judge, ensure that there will be an appropriate, yet practical, sample upon which to base the verdict (decision).

Contrary to the popular misconception, a person found “not guilty” has not been proven “innocent.”  Rather, the “not guilty” verdict means that the evidence presented at trial was not enough for all twelve jurors, beyond a reasonable doubt, to reject the null hypothesis (not guilty) and accept the alternative hypothesis (guilty).  Serving on a jury carries tremendous responsibility, as there is always a finite chance that the wrong verdict will be reached (because no decision can be made with 100% certainty).  The stipulation that a unanimous jury must decide guilt beyond a reasonable doubt is designed to reduce the risk of finding a not guilty defendant guilty by putting the rights of the individual above the interest of the State. To wit: “It is better to let the crime of a guilty person go unpunished than to condemn the innocent.”[1]

Having considered the Hypothesis Test through the lens of the legal system, let us now examine a general case applied to science.  A graphical representation of the Hypothesis Test, sprinkled with the lingo of engineering statistics (familiar to Six Sigma practitioners), is shown in Figure 1.

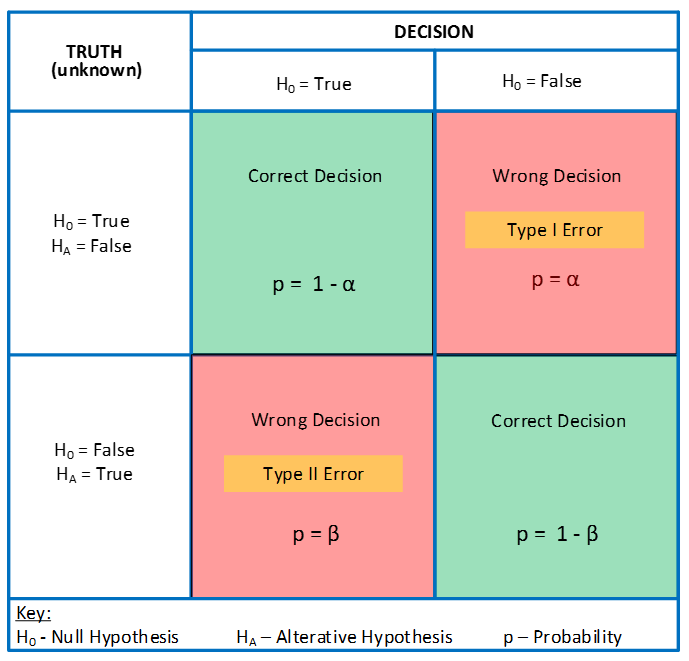Figure 1: General Hypothesis Test

Innocent Until Proven Guilty: Hypothesis Test (con't): The left-most column, labeled “TRUTH,” is key to appreciating the necessity of a scientifically sound approach to decision-making:  The TRUTH is and will always be, unknown.  For each row of TRUTH, the 100% probability of making a decision is split between the Correct Decision and the Wrong Decision.  Thus, a scientifically sound approach to decision-making requires systematic evaluation of the four possible “DECISION” outcomes.  A good starting point is to consider the consequences of a Wrong Decision, including which of the two possible errors (Type I or Type II) is the worst, an understanding of which enables leaders to direct resources toward minimizing its likelihood.  In the criminal justice system example, the rules and routines protect the rights of the accused to avoid the gross injustice of finding a not guilty person, guilty (Type II Error).[2]

In summary, Hypothesis Test principles are not merely handy guidelines by which engineers should operate. They should be systematically applied at all levels of an organization. To set the tone, senior leadership should require evidence that resources are appropriately allocated to ensure that increased Patient Safety Risk is detected (Power), should it occur, and engineers should ensure that process alarms don’t force unnecessary process interventions (Type II Error).  In all cases, the question being asked—i.e., the hypotheses being posed—must be clearly stated; a common understanding of the consequences of an incorrect decision achieved; and resources allocated to ensure a valid result is attained.

As illustrated above, foundational to such efforts is a firm grasp of Hypothesis Test fundamentals.

___________________________________

[1] From an 1895 U.S. Supreme Court case, cited in NCJRS 209545
[2] The system is also designed to arrive at the Correct Decision when the defendant is guilty.  The probability of doing so is p = 1 - β or “Power”, in engineering statistics.  See the blog, “The Power to See Differences that Matter” for a detailed treatment of Power.

Interested in learning more? Contact us today to find out how we can help with your global regulatory needs.